Trigonometry may seem intimidating at first, but by exploring its basic concepts using JavaScript, we can gain a better understanding of how it works.

With trigonometric functions like sine, cosine, and tangent, we can solve a wide range of problems in mathematics, science, engineering, and beyond. So next time you encounter a triangle, remember that JavaScript can help you unlock its secrets through the power of trigonometry.

The Unit Circle

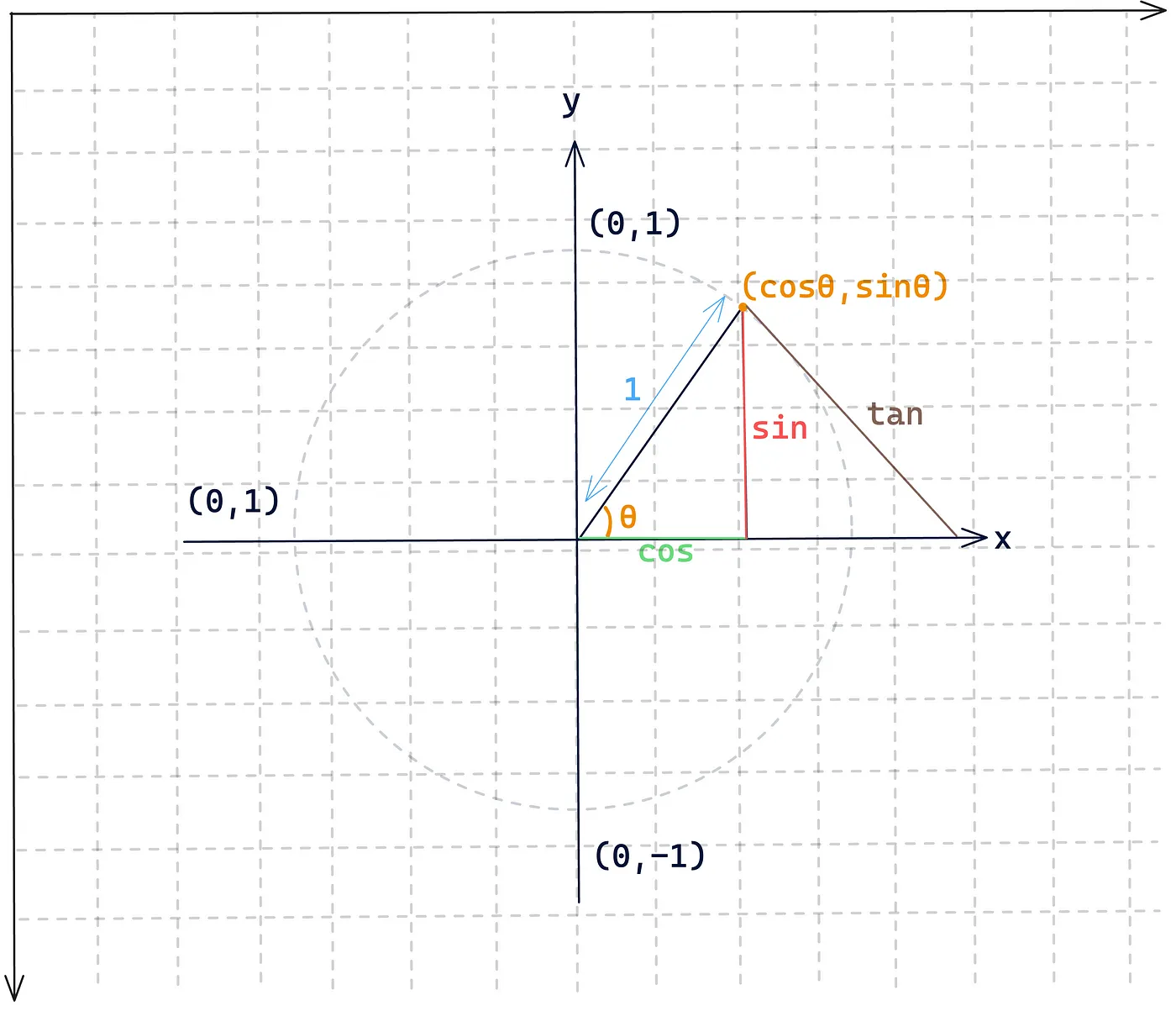
The unit circle is a circle with a radius of 1, centered at the origin (0, 0) of a Cartesian coordinate system.

Degree And Radian

While degrees are more commonly used in everyday contexts, radians are often preferred in mathematical calculations due to their convenient relationship with the properties of circles and trigonometric functions. There are 2pi radians in a circle.

Sine (sin): The sine of an angle is the ratio of the length of the side opposite that angle to the length of the hypotenuse.

const angleInRadians = Math.PI / 6 // 30 degrees in radians
Math.sin(angleInRadians) // Output: 0.5

Cosine (cos): The ratio of the length of the side adjacent to an angle to the length of the hypotenuse.

const angleInRadians = Math.PI / 3 // 60 degrees in radians
Math.cos(angleInRadians) // Output: 0.5

Tangent (tan): The ratio of the length of the side opposite an angle to the length of the side adjacent to the angle.

const angleInRadians = Math.PI / 4 // 45 degrees in radians
Math.tan(angleInRadians) // Output: 1

Polar Coordinates

The polar coordinate system is an alternative coordinate system used to specify the location of points in a plane.

Unlike the Cartesian coordinate system, which uses x and y coordinates to locate a point, the polar coordinate system uses a distance (radius) and an angle to describe the position of a point relative to a reference point (origin).

Let’s Draw

We will draw a simple visualization of a polar coordinate system with JavaScript Canvas API We start by visualizing a circle, x-axis and y-axis on the Canvas center

const canvas = document.getElementById('myCanvas')
const ctx = canvas.getContext('2d')
const r = 100
const originX = canvas.width / 2
const originY = canvas.height / 2
ctx.beginPath()
ctx.strokeStyle = 'black'
ctx.arc(originX, originY, r, 0, 2 * Math.PI)
ctx.lineWidth = 2
ctx.stroke()

ctx.beginPath()
ctx.moveTo(originX, 50)
ctx.lineTo(originX, canvas.height - 50)
ctx.stroke()

ctx.beginPath()
ctx.moveTo(50, canvas.height / 2)
ctx.lineTo(canvas.height - 50, originX)
ctx.stroke()

After we drew a circle and x/y-axis on the canvas can draw a point according to the mouse position on the circle. We need sinus, cosine and radian values for the point position

function getMousePos(canvas, e) {
  const rect = canvas.getBoundingClientRect()
  return {
    x: e.clientX - rect.left,
    y: e.clientY - rect.top
  }
}

function calculate(deltaX, deltaY) {
  const angle = (Math.atan2(deltaY, deltaX) * 180) / Math.PI
  const radian = (Math.round(angle) / 360) * (2 * Math.PI)
  const cos = originX + r * Math.cos(rad)
  const sin = originY + r * Math.sin(rad)
  return {
    cos,
    sin,
    radian
  }
}

Conclusion

Whether you’re building educational tools, gaming experiences, or data visualization applications, understanding and leveraging trigonometry in JavaScript can elevate your projects to new heights, offering users immersive and engaging experiences on the web. I will continue to write new articles on this subject.

Thank you for reading and feedback 🙏